یکی از خوانندگان وبلاگ این سوال رو از من پرسیده:
"سلام.خسته نباشید.من دانشجو ارشد برق هستم.زمانی که که واس کنکور درس ریاضی مهندسی رو میخوندم توی قسمت انتگرال مختلط همش واسم سوال بود که این عددی که بدست میارم چیه اصلا>مساحته؟حجمه؟طوله؟.توی انتگرالهای یگانه که مساحت زیر نمودار به دست می آد ولی انتگرال مختلطو درک نکردم هنوز.اگه میشه راهنمایی کنین.توی قسمت انتگرال روی منحنی و روی سطح ریاضی2 هم متوجه نشدم چیو دارم حساب میکنم.ممنون میشم اگه راهنمایی کنید."
-----------------------------------------
در مورد انتگرال مختلط بزارید اول خیالتون رو راحت کنم که هیج تعبیر هندسی و یا فیزیکی مفیدی نداره و در واقع یک تعمیم سر راست از انتگرال توابع حقیقی هست. در کتاب توابع مختلط نوشته چرچیل که معروفترین رفرنس درس توابع مختلط در سطح دانشگاه هاست در انتهای بخش 40 این کتاب نوشته شده:
"Definite integrals in calculus can be interpreted as areas, and they have other interpretations as well. Except in special cases, no corresponding helpful interpretation, geometric or physical, is available for integrals in the complex plane"
البته این به معنی مفید نبودن انتگرال مختلط نیست!!! مثلا فرم کلی تبدیل لاپلاس معکوس رو میشه به شکل یک انتگرال مختلط نوشت (به بخش 88 کتاب توابع مختلط چرچیل ویرایش هشتم رجوع کنید) و یا بعضی از انتگرال های حقیقی رو که با روش های عادی نمیشه حساب کرد؛ میشه به فرم مختلط جواب اونها رو به دست اوورد که احتمالا این موضوع رو در درس ریاضیات مهندسی دیدید.
اما برای اینکه به هر حال بدونیم این عددی که توی انتگرال مختلط به دست میاد چی رو نشون میده و اصلا چی هست. اول باید برگردیم به مفهوم ضرب اعداد مختلط. هر عدد مختلط چیزی جز یک بردار در صفحه نیست و بنابراین یک طول داره و یک زاویه با جهت مثبت محور ایکس ها: وقتی که دو عدد مختلط

رو در هم ضرب می کنیم به یک عدد مختلط می رسیم که اندازه اش به اندازه حاصلضرب این دو عدد مختلط هست و زاویه اش با محور ایکس ها برابر مجموع زوایای این دو بردار هست.یعنی

اما از طرفی انتگرال تابع مختلط  روی مسیر
روی مسیر  رو میشه به صورت زیر در نظر گرفت:
رو میشه به صورت زیر در نظر گرفت:

اونوقت براساس چیزهایی که تا اینجا گفتم معنی  با کمی اغماض این میشه:
با کمی اغماض این میشه:
" اگر به هر نقطه از مسیر  برداری به نام
برداری به نام  که از دوران بردار
که از دوران بردار  به اندازه زوایه شیب خط مماس بر منحنی
به اندازه زوایه شیب خط مماس بر منحنی  در آن نقطه به دست میآید نسبت دهیم؛ و بعد میانگین این بردارهای
در آن نقطه به دست میآید نسبت دهیم؛ و بعد میانگین این بردارهای  را حساب کنیم
را حساب کنیم  به دست میاید."
به دست میاید."
خلاصه همه این حرف ها اینه که: " انتگرال گیری مختلط: محاسبه میانگین بردارها است." (که این بردارها به مفهومی که در بالا گفتم هستند).
---------
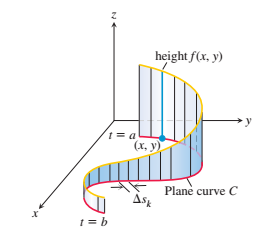
در مورد قسمت بعد سوال که تعبیر انتگرال خط و انتگرال سطح چیه؛ تو اغلب کتاب های ریاضی عمومی به طور مفصل این موضوعات توضیح داده شده (مثلا کتاب ریاضیات عمومی توماس). مثلا در مورد انتگرال خط روی مسیر  ؛ فرض کنید روی این منحنی دیواری ساخته شده که ارتفاع دیوار در هر نقطه ی منحنی ؛ برابر مقدار تابع
؛ فرض کنید روی این منحنی دیواری ساخته شده که ارتفاع دیوار در هر نقطه ی منحنی ؛ برابر مقدار تابع  تو اون نقطه باشه. در این صورت انتگرال خط تابع
تو اون نقطه باشه. در این صورت انتگرال خط تابع  روی این مسیر
روی این مسیر  برابر است با مساحت دیوار است.
برابر است با مساحت دیوار است.
پ ن: اگر در آینده فرصت کنم؛ یک ویدیو با متلب و یا کتابخانه matplotlib پایتون می سازم (هیچی مثل پایتون نمی تونه خوب نمودار بکشه!!!)که مفهوم انواع انتگرال ها رو به صورت یک انیمیشن نشون بدم. شاید توی عید فرصت این کار فراهم بشه. به شرطی که تا اون موقع انجام این موضوع یادم نره!!!

